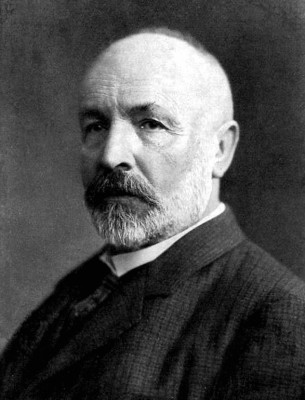Splitting Infinity(ves): The Story of Georg Cantor

3/7/2016

In mathematics, it was always assumed that everything is based on our rational understanding of logic and common sense. Unlike physics, which can get extremely esoteric, mathematics limits itself how abstract our understanding of logic can get.

But once in a while there are those who cross over that limit, into fields that borders on pseudoscience such as numerology. Gerge Cantor was such a person.

"The fear of infinity is a form of myopia that destroys the possibility of seeing the actual infinite, even though it in its highest form has created and sustains us, and in its secondary transfinite forms occurs all around us and even inhabits our minds." - Georg Cantor

If we were to imagine the largest possible number, what would you call that? Colloquial wisdom would immediately name it ‘infinity’. But the idea of infinity is not so much about size as it is more about volume. Just as a balloon filled with air may be just as large as a balloon filled with water, volume counts. For quite some time, mathematicians had resigned that the idea of infinity is just an abstract, conceptual novelty. Pi, for instance, is theorized to have an infinite string of numerical decimals; even astronomers calculating the curvature of the universe only need about 30 decimal points.

But for those practicing pure mathematics (i.e. math for math’s sake), infinity is serious business. 'Infinity' by its technical, mathematical definition is something which is equal to some of its parts. Infinity became a really clear and well-defined quantity mathematically in the late 19th century, which it wasn't before and which makes it rather different from what we ordinarily talk about when we talk about infinity, namely, about something very, very big. In mathematics nowadays, when we think about infinity, we think about a mathematical set whose properties are different from those of ordinary sets.

The defining property of infinity today is that a set's cardinality (the number of elements in a given mathematical set) is equal to the cardinality of some real subset of that set. The thread that links the technical notion of infinity and the more popular/philosophical notion of infinity is the sense that infinity's hugeness being beyond reach endows it with certain paradoxical properties.

An example would be what was taken to be something rather paradoxical, the fact that you can take, say, the number 1 and correlate it with the number 2, take the number 2 and correlate it with the number 4, take the number 3 and correlate it with the number 6. In this way you can gradually, step by step, correlate all integer numbers (1, 2, 3, 4, etc.) with all even numbers (2, 4, 6, 8, etc.). And that's funny, because this would imply at first glance that the number of integers is equal to the number of even integers. That's the paradoxical property of infinity.

In the 17th Century, Galileo had tried to confront the idea of infinity and the apparent contradictions thrown up by comparisons of different infinities, but in the end shied away from the problem. He had shown that a one-to-one correspondence (1-2, 3-4, 5-6, …) could be drawn between all the natural numbers and the squares of all the natural numbers to infinity, suggesting that there were just as many square numbers as integers, even though it was intuitively obvious there were many integers that were not squares, a concept which came to be known as Galileo’s Paradox.

In the 1874, a 29 year old German mathematician published an article that was to be the beginning of a new branch of mathematics, set theory. Georg Ferdinand Ludwig Philipp Cantor’s article, On a Property of the Collection of All Real Algebraic Numbers, sets to prove that one can always list down a series on number no matter how far down the infinite path one goes.

Cantor's starting point was to say that, if it was possible to add 1 and 1, or 25 and 25, etc, then it ought to be possible to add infinity and infinity. He realized that it was actually possible to add and subtract infinities, and that beyond what was normally thought of as infinity existed another, larger infinity, and then other infinities beyond that. In fact, he showed that there may be infinitely many sets of infinite numbers - an infinity of infinities - some bigger than others, a concept which clearly has philosophical, as well as just mathematical, significance. The sheer audacity of Cantor’s theory set off a quiet revolution in the mathematical community, and changed forever the way mathematics is approached.

His first intimations of all this came in the early 1870s when he considered an infinite series of natural numbers (1, 2, 3, 4, 5, ...), and then an infinite series of multiples of ten (10, 20 , 30, 40, 50, ...). He realized that, even though the multiples of ten were clearly a subset of the natural numbers, the two series could be paired up on a one-to-one basis (1 with 10, 2 with 20, 3 with 30, …) – the same process that Galileo used - to show that they were the same “sizes” of infinite sets, in that they had the same number of elements.

This clearly also applies to other subsets of the natural numbers, such as the even numbers 2, 4, 6, 8, 10, etc, or the squares 1, 4, 9, 16, 25, etc, and even to the set of negative numbers and integers. In fact, Cantor realized that he could, in the same way, even pair up all the fractions (or rational numbers) with all the whole numbers, thus showing that rational numbers were also the same sort of infinity as the natural numbers, despite the intuitive feeling that there must be more fractions than whole numbers.

However, when Cantor considered an infinite series of decimal numbers, which includes irrational numbers like π, e and √2, this method broke down. He used several clever arguments (one being the "diagonal argument" explained in the box on the right) to show how it was always possible to construct a new decimal number that was missing from the original list, and so proved that the infinity of decimal numbers (or, technically, real numbers) was in fact bigger than the infinity of natural numbers.

He also showed that they were “non-denumerable” or "uncountable" (i.e. contained more elements than could ever be counted), as opposed to the set of rational numbers which he had shown were technically (even if not practically) “denumerable” or "countable". In fact, it can be argued that there are an infinite number of irrational numbers in between each and every rational number. The pattern less decimals of irrational numbers fill the "spaces" between the patterns of the rational numbers.

Just as importantly, though, this work of Cantor's between 1874 and 1884 marks the real origin of set theory, which has since become a fundamental part of modern mathematics, and its basic concepts are used throughout all the various branches of mathematics. Although the concept of a set had been used implicitly since the beginnings of mathematics, dating back to the ideas of Aristotle, this was limited to everyday finite sets. In contradistinction, the “infinite” was kept quite separate, and was largely considered a topic for philosophical, rather than mathematical, discussion. Cantor, however, showed that, just as there were different finite sets, there could be infinite sets of different sizes, some of which are countable and some of which are uncountable.

Throughout the 1880s and 1890s, he refined his set theory, defining well-ordered sets and power sets and introducing the concepts of ordinality and cardinality and the arithmetic of infinite sets. What is now known as Cantor's theorem states generally that, for any set A, the power set of A (i.e. the set of all subsets of A) has a strictly greater cardinality than A itself. More specifically, the power set of a countable infinite set is uncountably infinite.

Despite the central position of set theory in modern mathematics, it was often deeply mistrusted and misunderstood by other mathematicians of the day. One quote, usually attributed to Henri Poincaré, claimed that "later generations will regard Mengenlehre (set theory) as a disease from which one has recovered". Others, however, were quick to see the value and potential of the method, and David Hilbert declared in 1926 that "no one shall expel us from the Paradise that Cantor has created".

Cantor had few other mathematicians with whom he could discuss his ground-breaking work, and most were distinctly unnerved by his contemplation of the infinite. During the 1880s, he encountered resistance, sometimes fierce resistance, from mathematical contemporaries such as his old professor Leopold Kronecker and Henri Poincaré, as well as from philosophers like Ludwig Wittgenstein and even from some Christian theologians, who saw Cantor's work as a challenge to their view of the nature of God. Cantor himself, a deeply religious man, noted some annoying paradoxes thrown up by his own work, but some went further and saw it as the willful destruction of the comprehensible and logical base on which the whole of mathematics was based.

As he aged, Cantor suffered from more and more recurrences of mental illness, which some have directly linked to his constant contemplation of such complex, abstract and paradoxical concepts. In the last decades of his life, he did no mathematical work at all. He spent long periods in the Halle sanatorium recovering from attacks of manic depression and paranoia, and it was there, alone in his room, that he finally died in 1918, his great project still unfinished.

Ponder this

We mentioned numerology, the disproved notion that numbers holds esoteric secrets. Why was it discredited? How is Cantor's approach on number theory different from numerology?

What are the common grounds between the philosophical notions on infinity and those in mathematics?

Discuss

Some have dismissed pure mathematics as nothing more than academic exercises, and railed against the abstract and therefore inapplicable nature of it. Were there cases where pure mathematics became relevant in applied mathematics (e.g. statistics, computing, actuarial science)?