|
Have you ever went through a wild goose chase? Trolled into looking for something that was never there? Well then you'd understand how generations of mathematicians, spanning more than three centuries felt as they became part of the mathematical world's greatest practical joke: Pierre de Fermat's last theorem.
U mad bro? |
"Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caperet."
Pierre de Fermat, handwritten on a copy of Diophantus' Arithmetica, 1637
Fermat's Last Theorem is a very famous idea in mathematics. It says that: x^n + y^n = z^n is false, where x, y and z are different whole numbers, and n is larger than 2.
If n is a whole number which is higher than 2 (like 3, 4, 5, 6.....), then the equation has no solutions when x, y and z are natural numbers (positive whole numbers (integers) or 'counting numbers' such as 1, 2, 3....). This means that there are no natural numbers x, y and z for which this equation is true (that is, the values on both sides can never be the same if x, y, z are natural numbers and n is an integer higher than 2).
Pierre de Fermat wrote about it in 1637 inside his copy of a book called Arithmetica. He said "I have discovered a truly remarkable proof of this theorem which this margin is too small to contain." However, no correct proof was found for 357 years. Mathematicians everywhere think that Fermat, in fact, did not have a good proof of this theorem.
If n is a whole number which is higher than 2 (like 3, 4, 5, 6.....), then the equation has no solutions when x, y and z are natural numbers (positive whole numbers (integers) or 'counting numbers' such as 1, 2, 3....). This means that there are no natural numbers x, y and z for which this equation is true (that is, the values on both sides can never be the same if x, y, z are natural numbers and n is an integer higher than 2).
Pierre de Fermat wrote about it in 1637 inside his copy of a book called Arithmetica. He said "I have discovered a truly remarkable proof of this theorem which this margin is too small to contain." However, no correct proof was found for 357 years. Mathematicians everywhere think that Fermat, in fact, did not have a good proof of this theorem.
|
History
The French mathematician Pierre de Fermat (1601-1665) was possibly the most productive mathematician of his era, making many contributions, some of which were to calculus, number theory, and the law of refraction. We will survey those contributions here, paying attention to his work in number theory. The following account of Fermat's background is taken from Mahoney's book, The Mathematical Career of Pierre de Fermat. Pierre de Fermat was born on August 17, 1960, in Beaumont-de-Lomagne, a small town near Toulouse in the south part of France, near the border with Spain. His father, Dominique Fermat, was a wealthy leather merchant who held the position of "second consul" of Beaumont-de-Lomagne, a governmental position similar to the position of mayor in our time. His mother, Claire, née de Long, was the daughter of a prominent family. Fermat had a brother, Clément, and two sisters, Louise and Marie. While relatively little is known of Fermat's early education, it is known that he was of Basque origin and received his primary and secondary education at the monastery of Grandslve, run by the Cordeliers (Franciscans), in Beaumont-de-Lomagne. For his advanced studies he first attended the University of Toulouse before moving to Bordeaux in the second half of the 1620's. In Bordeaux (1629) Fermat began his first serious mathematical researches, where he gave a copy of his restoration of Appollonius's Plane Loci to one of the mathematicians there. In Bordeaux he contacted Beaugrand and during this time he produced work on maxima and minima. He gave his work to Etienne de l'Espagnet, who shared mathematical interests with Fermat. |
From Bordeaux, Fermat went to study law at the University of Orléans. On May 1631, he received the degree in Civil Laws. Fermat's choice of a legal career was natural and typical of his time, for his father's wealth and his mother's family background. To be in this career was an avenue to a higher social status and political power. After graduating he purchased the office of councillor at the parliament in Toulouse. Soon after that he acquired a wife. She was his cousin fourth removed, Louise de Long. He gave a dowry of 12,000 livres (the French currency at the time), which was not a problem for the young lawyer. Soon after, he served in the local parliament and became councillor, or legislator. His entire family, now including his father-in-law, were members of the upper class. Mahoney tells us how this affected his social status as well.
Very little is known about Fermat's private life. He had five children, Clément-Samuel, Jean, Claire, Catherine, and Louise. Clément-Samuel was the oldest and closest to Fermat. He may have shared many mathematical interests with Fermat. Clément-Samuel eventually inherited his father's office of councillor.
For the remainder of his life Fermat lived in Toulouse, but he also worked in his hometown of Beaumont-de-Lomagne, and the nearby town of Castres. First he worked in the lower chamber of Parliament, but then in 1638 he was appointed to the higher chamber, and finally in 1652 he was promoted to the highest level in the criminal court. This position was usually given to people of seniority, but since the plague had struck in the early 1650's, many of the older men had died. Fermat himself was struck down with the plague. In 1653 his death was wrongly reported; Fermat had survived. This account of Fermat's background and life was taken from.
Fermat contributed to the development of the calculus through his work on the properties of curves. He found the areas bounded by these curves, though a summation process. As Bell states, "The creators of calculus, including Fermat, relied on geometric and physical (mostly kinematical and dynamical) intuition to get them ahead: they looked at what passed in their imaginations for the graph of a continuous curve..."
We now call this process integral calculus. It is ironic that Fermat did not see what we now call the Fundamental Theorem of Calculus. However, his work on this subject was an aid to developing the differential calculus. In addition to his contribution to calculus, Fermat contributed to the law of refraction. He had a disagreement with the philosopher and amateur mathematician, René Descartes. "According to [Fermat's] principle, if a ray of light passes from a point A to another point B, being reflected and refracted(refracted; that is, bent, as in passing from air to water, or through a jelly of variable density) in any manner during the passage, the path which it must take can be calculated- all its twistings and turnings due to the refraction, and all its dodgings back and forth due to reflections- from the single requirement that the time taken to pass from A to B shall be an extreme."
Descartes was trying to justify the sine law (Snell's law) by saying that light travels more rapidly in the denser of the two media involved in the refraction. Twenty years later Fermat realized that this appeared to conflict with the Aristotelian view that nature always chooses the shortest path.
Fermat applied his method of maxima and minima and assumed that light travels less rapidly in the medium. He showed that the law of refraction is consistent with the principle of least time. From this principle Fermat deduced the familiar laws of reflection and refraction: the angle of reflection; the sine of the angle of incidence (in refraction) is a constant number times the sine of the angle of refraction in passing from one medium to anoint her.
Finally, there’s Fermat's last discovery, his Last Theorem. While he was reading a copy of Diophantus' Arithmetica, Fermat made a marginal note that remained unsolved until very recently. He read the eighth problem in Dipohantus's book, which asks for the solution in rational numbers of the equation x2 + y2= a2. According to Bell, Fermat says "on the contrary, it is impossible to separate a cube into two cubes, a fourth power into two fourth powers, or generally, any power above the second into two powers of the same degree: I have discovered a truly marvelous demonstration [of this general theorem] which this margin is too narrow to contain"
Fermat’s Last Theorem
Fermat's Last Theorem is a more general form of the equation: x^n + y^n = z^n. (This comes from the Pythagorean theorem). A special case is when a, b, and c are whole numbers. Then they are named a "Pythagorean triple". There are an infinite number of them (they go on forever). Fermat's Last Theorem talks about what happens when the 2 changes to a bigger whole number. It says that then there are no triples when a, b, and c are integers greater than or equal to one (meaning that if n is more than three, a, b and c cannot be natural numbers).
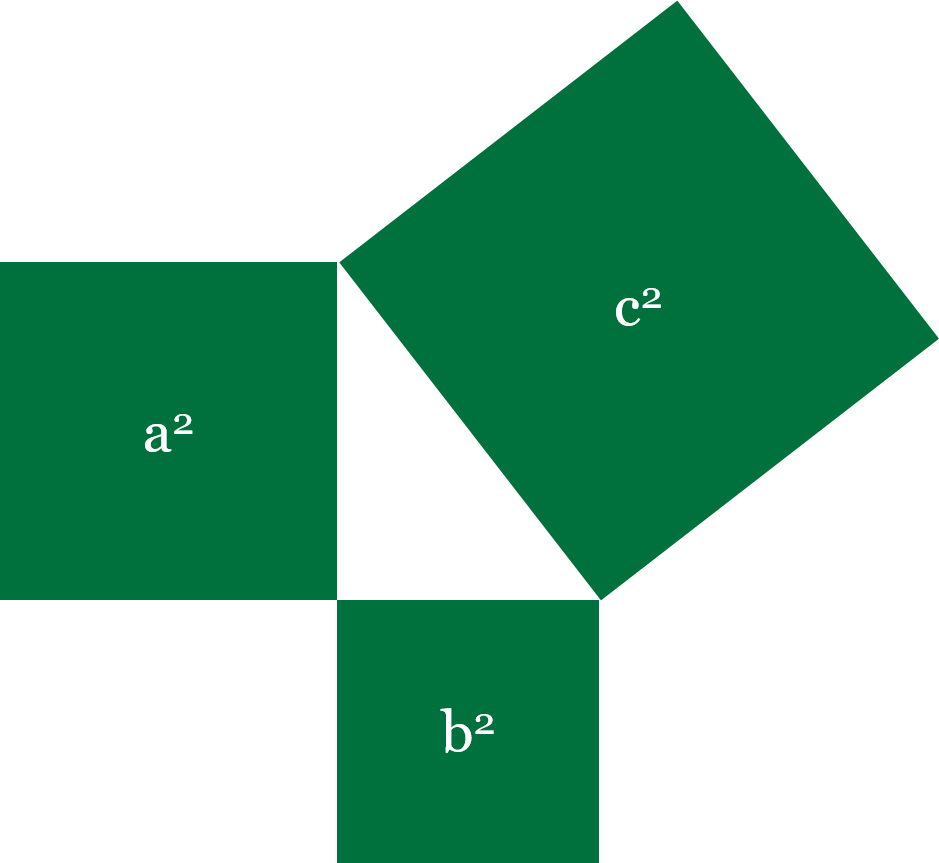
If we were to visualize, Pythagoras' theorem, we'll get something like this.
Very little is known about Fermat's private life. He had five children, Clément-Samuel, Jean, Claire, Catherine, and Louise. Clément-Samuel was the oldest and closest to Fermat. He may have shared many mathematical interests with Fermat. Clément-Samuel eventually inherited his father's office of councillor.
For the remainder of his life Fermat lived in Toulouse, but he also worked in his hometown of Beaumont-de-Lomagne, and the nearby town of Castres. First he worked in the lower chamber of Parliament, but then in 1638 he was appointed to the higher chamber, and finally in 1652 he was promoted to the highest level in the criminal court. This position was usually given to people of seniority, but since the plague had struck in the early 1650's, many of the older men had died. Fermat himself was struck down with the plague. In 1653 his death was wrongly reported; Fermat had survived. This account of Fermat's background and life was taken from.
Fermat contributed to the development of the calculus through his work on the properties of curves. He found the areas bounded by these curves, though a summation process. As Bell states, "The creators of calculus, including Fermat, relied on geometric and physical (mostly kinematical and dynamical) intuition to get them ahead: they looked at what passed in their imaginations for the graph of a continuous curve..."
We now call this process integral calculus. It is ironic that Fermat did not see what we now call the Fundamental Theorem of Calculus. However, his work on this subject was an aid to developing the differential calculus. In addition to his contribution to calculus, Fermat contributed to the law of refraction. He had a disagreement with the philosopher and amateur mathematician, René Descartes. "According to [Fermat's] principle, if a ray of light passes from a point A to another point B, being reflected and refracted(refracted; that is, bent, as in passing from air to water, or through a jelly of variable density) in any manner during the passage, the path which it must take can be calculated- all its twistings and turnings due to the refraction, and all its dodgings back and forth due to reflections- from the single requirement that the time taken to pass from A to B shall be an extreme."
Descartes was trying to justify the sine law (Snell's law) by saying that light travels more rapidly in the denser of the two media involved in the refraction. Twenty years later Fermat realized that this appeared to conflict with the Aristotelian view that nature always chooses the shortest path.
Fermat applied his method of maxima and minima and assumed that light travels less rapidly in the medium. He showed that the law of refraction is consistent with the principle of least time. From this principle Fermat deduced the familiar laws of reflection and refraction: the angle of reflection; the sine of the angle of incidence (in refraction) is a constant number times the sine of the angle of refraction in passing from one medium to anoint her.
Finally, there’s Fermat's last discovery, his Last Theorem. While he was reading a copy of Diophantus' Arithmetica, Fermat made a marginal note that remained unsolved until very recently. He read the eighth problem in Dipohantus's book, which asks for the solution in rational numbers of the equation x2 + y2= a2. According to Bell, Fermat says "on the contrary, it is impossible to separate a cube into two cubes, a fourth power into two fourth powers, or generally, any power above the second into two powers of the same degree: I have discovered a truly marvelous demonstration [of this general theorem] which this margin is too narrow to contain"
Fermat’s Last Theorem
Fermat's Last Theorem is a more general form of the equation: x^n + y^n = z^n. (This comes from the Pythagorean theorem). A special case is when a, b, and c are whole numbers. Then they are named a "Pythagorean triple". There are an infinite number of them (they go on forever). Fermat's Last Theorem talks about what happens when the 2 changes to a bigger whole number. It says that then there are no triples when a, b, and c are integers greater than or equal to one (meaning that if n is more than three, a, b and c cannot be natural numbers).
If we were to visualize, Pythagoras' theorem, we'll get something like this.
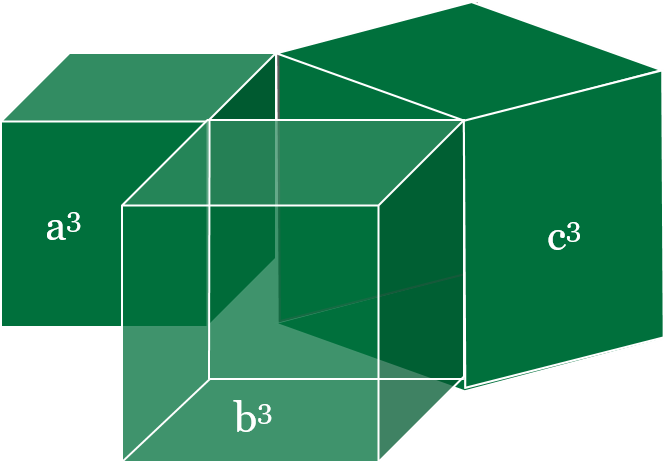
Fermat's idea is that such principles won't work with a power higher than 2. Naturally living in a 3D world, we can only visualize up to the power of 3, but you can see it doesn't seem to work.
Proof
The proof was made for some values of n (like n=3, n=4, n=5 and n=7). Fermat, Euler, Sophie Germain, and other people did this.
However, the full proof must show that the equation has no solution for all values of n (when n is a whole number bigger than 2). The proof was very difficult to find, and Fermat's Last Theorem needed lots of time to be solved.
An English mathematician named Andrew Wiles found a solution in 1995, 358 years after Fermat wrote about it. Richard Taylor helped him find the solution. The proof took eight years of research. He received the Wolfskehl Prize from Göttingen Academy in June 1997: it amounted to about $50,000 U.S. dollars.
After a few years of debate, people agreed that Andrew Wiles had solved the problem. Andrew Wiles used a lot of modern mathematics and even created new maths when he made his solution. This mathematics was unknown when Fermat wrote his famous note, so Fermat could not have used it. This leads one to believe that Fermat did not in fact have a complete solution of the problem.
The proof was made for some values of n (like n=3, n=4, n=5 and n=7). Fermat, Euler, Sophie Germain, and other people did this.
However, the full proof must show that the equation has no solution for all values of n (when n is a whole number bigger than 2). The proof was very difficult to find, and Fermat's Last Theorem needed lots of time to be solved.
An English mathematician named Andrew Wiles found a solution in 1995, 358 years after Fermat wrote about it. Richard Taylor helped him find the solution. The proof took eight years of research. He received the Wolfskehl Prize from Göttingen Academy in June 1997: it amounted to about $50,000 U.S. dollars.
After a few years of debate, people agreed that Andrew Wiles had solved the problem. Andrew Wiles used a lot of modern mathematics and even created new maths when he made his solution. This mathematics was unknown when Fermat wrote his famous note, so Fermat could not have used it. This leads one to believe that Fermat did not in fact have a complete solution of the problem.
Ponder this
Did Fermat actually solved the problem? Or was he really a troll?
In some ways we are being trolled right now. People have been telling us things that we take as truth, without even being presented the evidence for it. Do you know of anything like this in society?
Discuss
We embedded a trolling of our own in the article. Can you find it?
Further readings
Pierre de Fermat, a biography from The Story of Mathematics.
Visualising Fermat's Last Theorem, using computer graphics modelling to "see" the solution....if any.
Wiles's proof of Fermat's Last Theorem, a more detailed explanation of Wiles' Proof.
"Are mathematicians finally satisfied with Andrew Wiles's proof of Fermat's Last Theorem?", a 1999 article from the Scientific American magazine.