|
As ingenious as we are, humanity cannot escape the limits that physics have set upon in its laws. For a time at least. In this second part of the series on mechanical power, we will discover how human ingenuity games the laws of nature.
The limits are there, we just need to sidestep it with some clever thinking. |
“In practical terms the South Pointing Chariot was a simple direction finder. It could have been made to point in any direction - north, south, east or west.” – Kit Williams, "Engines of Ingenuity"
Power, as we have mentioned in the previous part of this series, is nothing if it can’t be controlled. In the previous part, we explained how power was transmitted, how it was harnessed using multiple gears of different sizes, in order to utilise it as efficiently and effectively as possible.
But the mechanics utilised in the real world is never a closed system. The laws of physics are all encompassing and it, as we, are subjected to it. At times we can do what we want with this new power, but for most of the time, we have to bow to it. But that does not mean we can’t bend the laws one in a while.
But the mechanics utilised in the real world is never a closed system. The laws of physics are all encompassing and it, as we, are subjected to it. At times we can do what we want with this new power, but for most of the time, we have to bow to it. But that does not mean we can’t bend the laws one in a while.
DISCLAIMER:
IFSA DOES NOT ENCOURAGE THE BREAKING OR BENDING OF ACTUAL LAWS IN THIS COUNTRY, WE’RE LAW ABIDING CITIZENS JUST LIKE MOST PEOPLE. WE IMPLORE THE MALAYSIAN GOVERNMENT NOT TO CHARGE US FOR CRIMINAL SEDITION JUST BECAUSE OUR AUTHORS ARE BEING OVERLY POETIC.
IFSA DOES NOT ENCOURAGE THE BREAKING OR BENDING OF ACTUAL LAWS IN THIS COUNTRY, WE’RE LAW ABIDING CITIZENS JUST LIKE MOST PEOPLE. WE IMPLORE THE MALAYSIAN GOVERNMENT NOT TO CHARGE US FOR CRIMINAL SEDITION JUST BECAUSE OUR AUTHORS ARE BEING OVERLY POETIC.
What we’re talking about is the differential. A special mechanical construction that allows the utilisation of power while allowing for the natural physical limitations to be abided.
A Problem
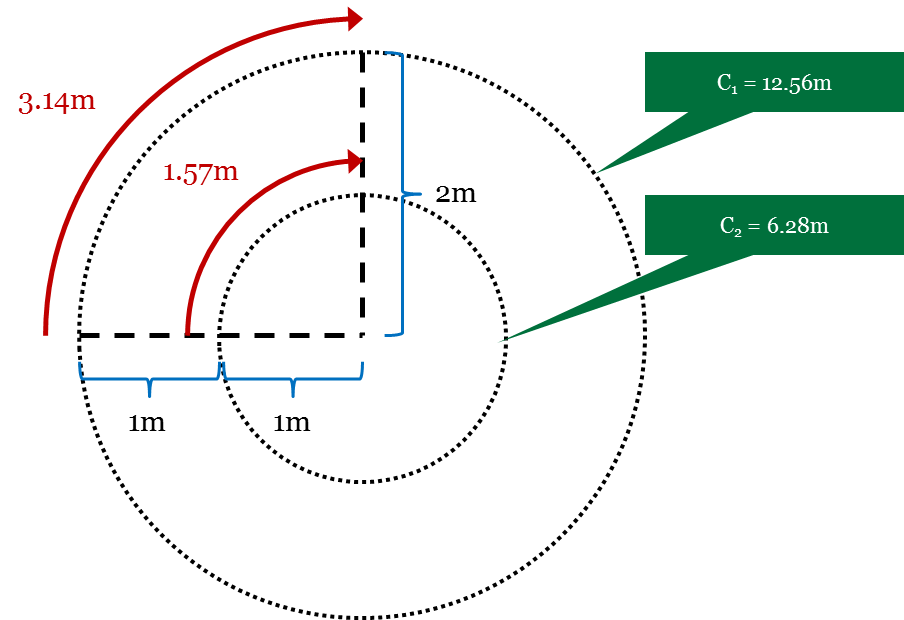
Let’s say that you’re driving down a road towards a turn, and you made that turn. What happens as you swerve around the curve towards another direction? Needless to say you would be following the curvature of the circumference of some circle. So what’s the big deal about that? For one, in both Euclidian and Non-Euclidian geometry, parts of the car will be traversing different lengths throughout the journey from 0° to 90°. For another, unlike the steering axle, the driving axle is connected to the transmission and ultimately the engine, and aren’t free to spin at whatever speed that suits the environment. An illustration:
A Problem
Let’s say that you’re driving down a road towards a turn, and you made that turn. What happens as you swerve around the curve towards another direction? Needless to say you would be following the curvature of the circumference of some circle. So what’s the big deal about that? For one, in both Euclidian and Non-Euclidian geometry, parts of the car will be traversing different lengths throughout the journey from 0° to 90°. For another, unlike the steering axle, the driving axle is connected to the transmission and ultimately the engine, and aren’t free to spin at whatever speed that suits the environment. An illustration:
As the analogy goes, no amount of power and control can make up for defying the laws of physics, let alone maths. Unless you can bend space, a single axle wheel set will either break (if there’s too much traction) or lose power (if too little) during the turn. There must be a win-win situation, no?
A History
Although ancient civilisations do not face this specific problem, as all wheels of their carriages or chariots are unpowered and free-wheeling (I made a joke!), it pops up in different situations.
Although it was never confirmed, it was suspected that something equivalent to the differential was used in the south-pointing chariots of Ancient China. This invention was created during the Three Kingdoms Era by Ma Jun (220 - 265) before the magnetic compass was invented, in order to aid travelers from getting lost in the vast, featureless plains in parts of China. Experimental historians had suspected that the directional integrity of the chariot was due to some mechanism to counter the torque given off as the chariot turns. Though due to the effects of friction, it may not be that reliable at great distances.
The first modern, documented use of a mechanism that allows for different rates of mechanical motion however, do not come from logistical needs, but horological. Back in the day before time was defined on a molecular scale, the sun was used as the arbiter in timekeeping. Because God can never make a mistake, right?
Thus a gentleman may need to readjust his watch from time to time, but may not have the access to an observatory, or just plain forgot to reset his watch. In 1720 a clockmaker, Joseph Williamson, sidestepped this need by incorporating the mechanism for readjustment into his clocks, problem is individual clocks are inaccurate at different rates, depending on their usage, temperature, or handling. Thus the first use of a differential was applied to allow for these differing rates to be corrected using pre-calculated and designed mechanism built into the clocks themselves.
This issue of mathematical applications arose again in the 19th century. With engineering becoming a full blown profession during the Industrial Revolution, the need to solve complex equations based on calculus, trigonometry, graph theory and differential rapidly and accurately brought the invention of mechanical computers. Contraptions such as Charles Babbage’s Analytical Engine, Martin Wiberg’s Logarithmic Calculator, and Vannevar Bush’s Differential Analyzer all use mechanism, in one form or another, to apply functions freely without causing delicate gears of their machines to jam or lock up – very much like our original vehicular example.
But the first use of the differential in a vehicle was invented by Onésiphore Pecqueur, a Frenchman (of course), in 1827. Not surprisingly the solution to the problem stated on top of this article was brought to us by a watchmaker. This revolutionary first application, to a steam-powered cart, provides the basis that allows for the safe and efficient use of mechanical power in transportation.
A History
Although ancient civilisations do not face this specific problem, as all wheels of their carriages or chariots are unpowered and free-wheeling (I made a joke!), it pops up in different situations.
Although it was never confirmed, it was suspected that something equivalent to the differential was used in the south-pointing chariots of Ancient China. This invention was created during the Three Kingdoms Era by Ma Jun (220 - 265) before the magnetic compass was invented, in order to aid travelers from getting lost in the vast, featureless plains in parts of China. Experimental historians had suspected that the directional integrity of the chariot was due to some mechanism to counter the torque given off as the chariot turns. Though due to the effects of friction, it may not be that reliable at great distances.
The first modern, documented use of a mechanism that allows for different rates of mechanical motion however, do not come from logistical needs, but horological. Back in the day before time was defined on a molecular scale, the sun was used as the arbiter in timekeeping. Because God can never make a mistake, right?
Thus a gentleman may need to readjust his watch from time to time, but may not have the access to an observatory, or just plain forgot to reset his watch. In 1720 a clockmaker, Joseph Williamson, sidestepped this need by incorporating the mechanism for readjustment into his clocks, problem is individual clocks are inaccurate at different rates, depending on their usage, temperature, or handling. Thus the first use of a differential was applied to allow for these differing rates to be corrected using pre-calculated and designed mechanism built into the clocks themselves.
This issue of mathematical applications arose again in the 19th century. With engineering becoming a full blown profession during the Industrial Revolution, the need to solve complex equations based on calculus, trigonometry, graph theory and differential rapidly and accurately brought the invention of mechanical computers. Contraptions such as Charles Babbage’s Analytical Engine, Martin Wiberg’s Logarithmic Calculator, and Vannevar Bush’s Differential Analyzer all use mechanism, in one form or another, to apply functions freely without causing delicate gears of their machines to jam or lock up – very much like our original vehicular example.
But the first use of the differential in a vehicle was invented by Onésiphore Pecqueur, a Frenchman (of course), in 1827. Not surprisingly the solution to the problem stated on top of this article was brought to us by a watchmaker. This revolutionary first application, to a steam-powered cart, provides the basis that allows for the safe and efficient use of mechanical power in transportation.
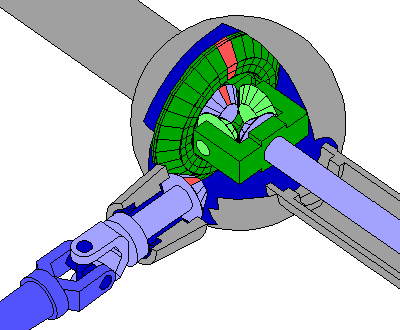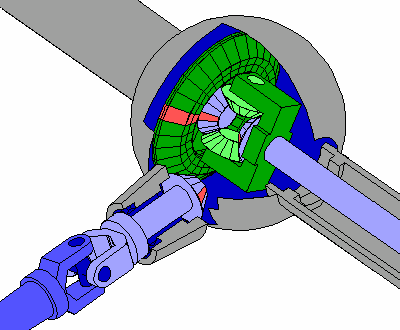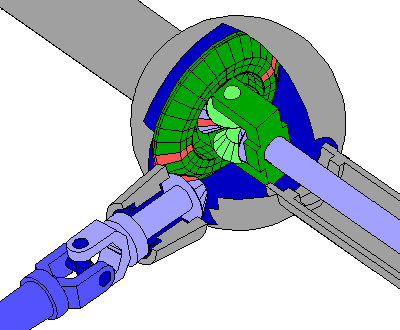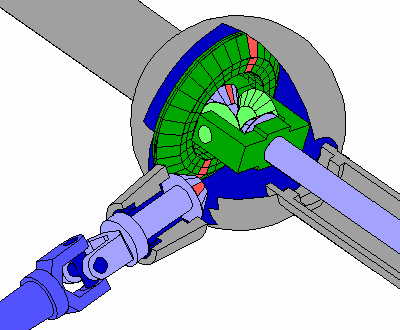
The Workings
In transportation, the differential have several purposes: (1) to provide power from the engine to the wheels; (2) to reduce the gears of the vehicle so that the rotational speed slows down before the wheels come to a complete stop; and (3) to allow the wheels to move freely at different speeds, hence the name. The differential essentially divides the force of the engine — the torque — in two ways so that the wheels can move in different speeds.
In transportation, the differential have several purposes: (1) to provide power from the engine to the wheels; (2) to reduce the gears of the vehicle so that the rotational speed slows down before the wheels come to a complete stop; and (3) to allow the wheels to move freely at different speeds, hence the name. The differential essentially divides the force of the engine — the torque — in two ways so that the wheels can move in different speeds.
|
This is necessary because without this feature, turning and changing directions become difficult to achieve. Wheels located on the inner section of the turn have less distance and slower speed to travel then the outer wheels. The differential remedies this by splitting the torque. Similarly, the front wheels move fast and have more distance to travel then the rear wheels. The differential also makes up for this.
Cars that consist of a set of wheels that drive and a set that don’t, however, do not suffer this problem. In this case, the wheels are not conjoined, so either the rear or the front wheels are capable of rotating independently. In the circumstance where there is no differential, the wheels are locked together and unable to produce simple, smooth turns, often relying on the slippage of a wheel to achieve this function. In order for a slip to occur, a great deal of traction is required between the car and the road. The weight of the force would have to be substantial to be transmitted from the axles to the wheels and would likely cause strain to the axles. |
Unlike common two-wheel drives, both four-wheel drive (4WD) and all-wheel drive (AWD) vehicles are usually designed in a certain way to meet the needs of both – providing power from the engine to both axles rather than just the rear. AWD, for example, requires differentials between each set of the wheels used for driving and also one between the front and the back wheels due to the fact that the front wheels travel a different distance.
In 4WD, the wheels all turn together simultaneously as they are connected by one differential. The obvious drawback of this type is that because the wheels are traveling at the same speed, regardless of the difference in distance between them, it becomes harder to turn in a direction, especially on concrete. In this case, the 4WD would have to be disengaged.
Future Context
The development of the differential is important as it introduces the concept of variability in power transmission. In the next article we will go back to the subject of transmission gears to see where this new idea eventually leads to.
In 4WD, the wheels all turn together simultaneously as they are connected by one differential. The obvious drawback of this type is that because the wheels are traveling at the same speed, regardless of the difference in distance between them, it becomes harder to turn in a direction, especially on concrete. In this case, the 4WD would have to be disengaged.
Future Context
The development of the differential is important as it introduces the concept of variability in power transmission. In the next article we will go back to the subject of transmission gears to see where this new idea eventually leads to.
Ponder this
We mentioned earlier that parallel curves differ in distances in Non-Euclidean geometry. We may have been mistaken. Try to prove whether this is true using epileptic and hyperbolic surfaces.
Ma Jun's differential was never described, although it serves the same function. How did he achieve this with a different design scheme?
Discuss
The differential is an example of mechanism that sacrifices power for more control. Similarly how the transmission gears trade off torque for speed and vice versa. But in both examples we have managed to optimize both (as compared to earlier designs). Would it be possible to design something where no trade-off is required?
Would we be sidestepping the laws of physics or is it a direct violation? What laws are involved in mechanical power transmissions? How can they be sidestepped?
Further readings
The differential, at Wikipedia
Ma Jun's south-pointing chariot, and Vannevar Bush's Differential Analyzer, non-automotive uses of the differential.
Pecqueur's differential, now used in the watch company bearing his name.