|
In 1990, a question was posed to a woman who happens to have the highest recorded IQ score in the world. Her answer sparked a debate among professional mathematicians of the day, and pits common sense against intellectual conventions.
I'm sure she felt goated for the failings of the arrogant eggheads at the time, pun intended... |
"The solution of the Monty Hall problem hinges on the concept of information, and more specifically, on the relationship between added information and probability."
Hans Christian von Baeyer, 'Information, The New Language of Science', 2003
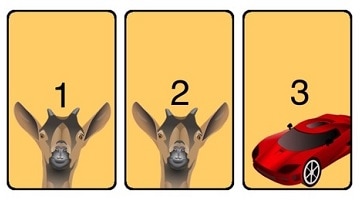
The Monty Hall problem is a famous problem in probability (chance). The problem is based on a television game show from the United States, Let's Make a Deal. It is named for the host of this show, Monty Hall.
In the problem, there are three doors. A car (prize of high value) is behind one door and goats (booby prizes of low value) behind the other two doors. First, the player chooses a door but does not open it. Then the host, who has knowledge of what is behind every door, opens a different door which they are certain has a goat behind it (opening either door with equal chances if the car is behind the player's door). Last, the host lets the player choose whether to keep what is behind the first door or to change choices to the third door (the one the host did not open). The rules of the problem are that the host has to open a door with a goat behind and has to let the player switch. The question is whether changing choices increases the chances of getting the car.
The chances of the car being behind the two doors that are still closed seem equal, so most people say changing choices does not increase the chances of getting the car. The true answer is that changing choices increases the chances of getting the car from 1/3 (one out of three) to 2/3 (two out of three).
That comes from the fact that the player, by choosing one door out of three, has a one chance in three of selecting the door with the car. The chance of the car being somewhere behind the other two doors is two out of three. So to improve their chance of winning a car, the player if given the choice, should swap their one door for the other two doors right away. But wait! The host then tries to confuse the player by opening one of their own goat doors. That changes nothing, remember that the player is still swapping their one door for the other two doors (even though one of them has been opened).
These are the options:
1. (Lose): If the player picks the car, then the host will show a goat. Then if the player changes their choice, they will get a goat .
2. (Win) : If the player picks a goat, then the host will show the other goat. Then if the player changes their choice, they will get a car.
3. (Win) : If the player picks the other goat, then the host will show the first goat. Then if the player changes their choice, they will get a car.
In the problem, there are three doors. A car (prize of high value) is behind one door and goats (booby prizes of low value) behind the other two doors. First, the player chooses a door but does not open it. Then the host, who has knowledge of what is behind every door, opens a different door which they are certain has a goat behind it (opening either door with equal chances if the car is behind the player's door). Last, the host lets the player choose whether to keep what is behind the first door or to change choices to the third door (the one the host did not open). The rules of the problem are that the host has to open a door with a goat behind and has to let the player switch. The question is whether changing choices increases the chances of getting the car.
The chances of the car being behind the two doors that are still closed seem equal, so most people say changing choices does not increase the chances of getting the car. The true answer is that changing choices increases the chances of getting the car from 1/3 (one out of three) to 2/3 (two out of three).
That comes from the fact that the player, by choosing one door out of three, has a one chance in three of selecting the door with the car. The chance of the car being somewhere behind the other two doors is two out of three. So to improve their chance of winning a car, the player if given the choice, should swap their one door for the other two doors right away. But wait! The host then tries to confuse the player by opening one of their own goat doors. That changes nothing, remember that the player is still swapping their one door for the other two doors (even though one of them has been opened).
These are the options:
1. (Lose): If the player picks the car, then the host will show a goat. Then if the player changes their choice, they will get a goat .
2. (Win) : If the player picks a goat, then the host will show the other goat. Then if the player changes their choice, they will get a car.
3. (Win) : If the player picks the other goat, then the host will show the first goat. Then if the player changes their choice, they will get a car.
So, it is true that if the player changes (switches) then the player will win a car two times out of three. When you switch, you win 2/3 of the time and lose 1/3, but when you don’t switch, you only win 1/3 of the time and lose 2/3. You can try it yourself and see.
Alternatively, you can actually play the game with another person acting as the host with three playing cards—two jokers for the goat and an ace for the prize. However, doing this a few hundred times to get statistically valid results can get a little tedious, so perhaps teachers can assign it as extra exam credits—or for punishment! But for convenience, here’s a flash version of the game, complete with statistical results.
Alternatively, you can actually play the game with another person acting as the host with three playing cards—two jokers for the goat and an ace for the prize. However, doing this a few hundred times to get statistically valid results can get a little tedious, so perhaps teachers can assign it as extra exam credits—or for punishment! But for convenience, here’s a flash version of the game, complete with statistical results.
The Intuitively Wrong “Solution”?
I didn't discuss what the general, incorrect, intuitive “solution” to this problem is: I didn't want to mislead, or confuse you. It was, in fact, my own initial response to this problem. In short, I felt that after Monty showed a losing door, that left two: one is right, the other wrong. It seemed to me, and to most people, that it's a 50:50 proposition: it doesn't matter if you switch, or not. Further, just to test instincts, One would ask oneself, “well, did Monty Hall reveal any information in opening the losing door?” And it seemed to me that he did not. But he did.
He did, because he always has to open a losing door: one losing door is always eliminated. The probabilities of your initial choice being correct, and the remaining choices have to sum to equal one. Therefore, the probability of the remaining choices have to sum to equal one minus the probability of your initial choice. In this case (with three doors), they have to sum to equal 2/3. Say a door isn't opened. Then, you would have two to switch to (if you choose to switch — this would be like “changing your mind”), and your chance of picking the correct door would be 1/2 × 2/3. Well, that's 1/3, just like your initial choice. But if Monty has to open a door, then you'll only have one door to switch to. In this case (which is the Monty Hall problem), you'll pick the remaining door — so that'd be 1 × 2/3. And that's a probability of 2/3.
If there were four doors, then your chance of being correct with your initial choice would be 1/4. The remaining doors would have the remaining probabilities: 3/4. Again, if no door were opened (“changing your mind”), you'd have to pick one of the three, and that'd be 1/3 × 3/4. That's 1/4, of course. But if an incorrect door were opened, you'd have only 2 to choose from. So that'd be 1/2 × 3/4. That's 3/8, which is better than 1/4. (1/4, which is the best you're going to do by “staying.”) So it's best to switch. ALWAYS.
If you are disheartened that your intuition led you astray, rest assured that you're in good company. It’s been noticed that the general tone in math puzzles is that only ignorant or stupid people fall for the incorrect solution to this puzzle. Don't you believe it. Many have argued about this puzzle with people that one might not expect to get the answer wrong: physicists, and generally very smart people, and even many mathematicians being confused by this problem.
I didn't discuss what the general, incorrect, intuitive “solution” to this problem is: I didn't want to mislead, or confuse you. It was, in fact, my own initial response to this problem. In short, I felt that after Monty showed a losing door, that left two: one is right, the other wrong. It seemed to me, and to most people, that it's a 50:50 proposition: it doesn't matter if you switch, or not. Further, just to test instincts, One would ask oneself, “well, did Monty Hall reveal any information in opening the losing door?” And it seemed to me that he did not. But he did.
He did, because he always has to open a losing door: one losing door is always eliminated. The probabilities of your initial choice being correct, and the remaining choices have to sum to equal one. Therefore, the probability of the remaining choices have to sum to equal one minus the probability of your initial choice. In this case (with three doors), they have to sum to equal 2/3. Say a door isn't opened. Then, you would have two to switch to (if you choose to switch — this would be like “changing your mind”), and your chance of picking the correct door would be 1/2 × 2/3. Well, that's 1/3, just like your initial choice. But if Monty has to open a door, then you'll only have one door to switch to. In this case (which is the Monty Hall problem), you'll pick the remaining door — so that'd be 1 × 2/3. And that's a probability of 2/3.
If there were four doors, then your chance of being correct with your initial choice would be 1/4. The remaining doors would have the remaining probabilities: 3/4. Again, if no door were opened (“changing your mind”), you'd have to pick one of the three, and that'd be 1/3 × 3/4. That's 1/4, of course. But if an incorrect door were opened, you'd have only 2 to choose from. So that'd be 1/2 × 3/4. That's 3/8, which is better than 1/4. (1/4, which is the best you're going to do by “staying.”) So it's best to switch. ALWAYS.
If you are disheartened that your intuition led you astray, rest assured that you're in good company. It’s been noticed that the general tone in math puzzles is that only ignorant or stupid people fall for the incorrect solution to this puzzle. Don't you believe it. Many have argued about this puzzle with people that one might not expect to get the answer wrong: physicists, and generally very smart people, and even many mathematicians being confused by this problem.
Ponder this
Are there any real life situations similar to this problem, or applications of its solution?
At the time the problem was presented, some of the most intelligent people got the answer wrong. How and why is that so?
Discuss
If there are any skeptics in the classroom, play the flash game provided. Discuss the cumulative mathematical odds of every round at every step.
Further readings
Monty Hall problem, at Wikipedia
Marilyn vos Savant, the person who brought the problem to light
"The Time Everyone “Corrected” the World’s Smartest Woman", an article on Marilyn vos Savant's attempt to tackle the problem
"A new approach to the Monty Hall problem", introduces the problem and tries to look at the problem in a new light