"There are no absolutes...in mathematics or in its history."
Eric Temple Bell, The Development of Mathematics (1940)
The history of mathematics is nearly as old as humanity itself. Since antiquity, mathematics has been fundamental to advances in science, engineering, and philosophy. It has evolved from simple counting, measurement and calculation, and the systematic study of the shapes and motions of physical objects, through the application of abstraction, imagination and logic, to the broad, complex and often abstract discipline we know today.
We shall begin our story from the notched bones of early man to the mathematical advances brought about by settled agriculture in Mesopotamia, where the most fundamental principles were born: numbers.
We shall begin our story from the notched bones of early man to the mathematical advances brought about by settled agriculture in Mesopotamia, where the most fundamental principles were born: numbers.
|
Prehistory
Our prehistoric ancestors would have had a general sensibility about amounts, and would have instinctively known the difference between, say, one and two antelopes. But the intellectual leap from the concrete idea of two things to the invention of a symbol or word for the abstract idea of "two" took many ages to come about. Even today, there are isolated hunter-gatherer tribes in Amazonia which only have words for "one", "two" and "many", and others which only have words for numbers up to five. In the absence of settled agriculture and trade, there is little need for a formal system of numbers. Early man kept track of regular occurrences such as the phases of the moon and the seasons. |
Some of the very earliest evidence of mankind thinking about numbers is from notched bones in Africa dating back to 35,000 to 20,000 years ago. But this is really mere counting and tallying rather than mathematics as such.
Pre-dynastic Egyptians and Sumerians represented geometric designs on their artefacts as early as the 5th millennium BCE, as did some megalithic societies in northern Europe in the 3rd millennium BCE or before. But this is more art and decoration than the systematic treatment of figures, patterns, forms and quantities that has come to be considered as mathematics.
Mathematics proper initially developed largely as a response to bureaucratic needs when civilizations settled and developed agriculture - for the measurement of plots of land, the taxation of individuals, etc - and this first occurred in the Sumerian and Babylonian civilizations of Mesopotamia (roughly, modern Iraq) and in ancient Egypt.
According to some authorities, there is evidence of basic arithmetic and geometric notations on the petroglyphs at Knowth and Newgrange burial mounds in Ireland (dating from about 3500 BCE and 3200 BCE respectively). These utilize a repeated zig-zag glyph for counting, a system which continued to be used in Britain and Ireland into the 1st millennium BCE. Stonehenge, a Neolithic ceremonial and astronomical monument in England, which dates from around 2300 BCE, also arguably exhibits examples of the use of 60 and 360 in the circle measurements, a practice which presumably developed quite independently of the sexagesimal counting system of the ancient Sumerian and Babylonians.
Sumerian & Babylonian Mathematics
Sumer (a region of Mesopotamia, modern-day Iraq) was the birthplace of writing, the wheel, agriculture, the arch, the plow, irrigation and many other innovations, and is often referred to as the Cradle of Civilization. The Sumerians developed the earliest known writing system - a pictographic writing system known as cuneiform script, using wedge-shaped characters inscribed on baked clay tablets - and this has meant that we actually have more knowledge of ancient Sumerian and Babylonian mathematics than of early Egyptian mathematics. Indeed, we even have what appear to school exercises in arithmetic and geometric problems.
Pre-dynastic Egyptians and Sumerians represented geometric designs on their artefacts as early as the 5th millennium BCE, as did some megalithic societies in northern Europe in the 3rd millennium BCE or before. But this is more art and decoration than the systematic treatment of figures, patterns, forms and quantities that has come to be considered as mathematics.
Mathematics proper initially developed largely as a response to bureaucratic needs when civilizations settled and developed agriculture - for the measurement of plots of land, the taxation of individuals, etc - and this first occurred in the Sumerian and Babylonian civilizations of Mesopotamia (roughly, modern Iraq) and in ancient Egypt.
According to some authorities, there is evidence of basic arithmetic and geometric notations on the petroglyphs at Knowth and Newgrange burial mounds in Ireland (dating from about 3500 BCE and 3200 BCE respectively). These utilize a repeated zig-zag glyph for counting, a system which continued to be used in Britain and Ireland into the 1st millennium BCE. Stonehenge, a Neolithic ceremonial and astronomical monument in England, which dates from around 2300 BCE, also arguably exhibits examples of the use of 60 and 360 in the circle measurements, a practice which presumably developed quite independently of the sexagesimal counting system of the ancient Sumerian and Babylonians.
Sumerian & Babylonian Mathematics
Sumer (a region of Mesopotamia, modern-day Iraq) was the birthplace of writing, the wheel, agriculture, the arch, the plow, irrigation and many other innovations, and is often referred to as the Cradle of Civilization. The Sumerians developed the earliest known writing system - a pictographic writing system known as cuneiform script, using wedge-shaped characters inscribed on baked clay tablets - and this has meant that we actually have more knowledge of ancient Sumerian and Babylonian mathematics than of early Egyptian mathematics. Indeed, we even have what appear to school exercises in arithmetic and geometric problems.
|
As in Egypt, Sumerian mathematics initially developed largely as a response to bureaucratic needs when their civilization settled and developed agriculture (possibly as early as the 6th millennium BCE) for the measurement of plots of land, the taxation of individuals, etc. In addition, the Sumerians and Babylonians needed to describe quite large numbers as they attempted to chart the course of the night sky and develop their sophisticated lunar calendar.
They were perhaps the first people to assign symbols to groups of objects in an attempt to make the description of larger numbers easier. They moved from using separate tokens or symbols to represent sheaves of wheat, jars of oil, etc, to the more abstract use of a symbol for specific numbers of anything. Starting as early as the 4th millennium BCE, they began using a small clay cone to represent one, a clay ball for ten, and a large cone for sixty. Over the course of the third millennium, these objects were replaced by cuneiform equivalents so that numbers could be written with the same stylus that was being used for the words in the text. A rudimentary model of the abacus was probably in use in Sumeria from as early as 2700 - 2300 BCE. |
|
Sumerian and Babylonian mathematics was based on a sexegesimal, or base 60, numeric system, which could be counted physically using the twelve knuckles on one hand the five fingers on the other hand. Unlike those of the Egyptians, Greeks and Romans, Babylonian numbers used a true place-value system, where digits written in the left column represented larger values, much as in the modern decimal system, although of course using base 60 not base 10.
Thus, 1 1 1 in the Babylonian system represented 3,600 plus 60 plus 1, or 3,661. Also, to represent the numbers 1 - 59 within each place value, two distinct symbols were used, a unit symbol (1) and a ten symbol (10) which were combined in a similar way to the familiar system of Roman numerals (e.g. 23 would be shown as 23). Thus, 1 23 represents 60 plus 23, or 83. However, the number 60 was represented by the same symbol as the number 1 and, because they lacked an equivalent of the decimal point, the actual place value of a symbol often had to be inferred from the context. |
It has been conjectured that Babylonian advances in mathematics were probably facilitated by the fact that 60 has many divisors (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60 - in fact, 60 is the smallest integer divisible by all integers from 1 to 6), and the continued modern-day usage of of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, are all testaments to the ancient Babylonian system. It is for similar reasons that 12 (which has factors of 1, 2, 3, 4 and 6) has been such a popular multiple historically (e.g. 12 months, 12 inches, 12 pence, 2 x 12 hours, etc).
The Babylonians also developed another revolutionary mathematical concept, something else that the Egyptians, Greeks and Romans did not have, a circle character for zero, although its symbol was really still more of a placeholder than a number in its own right.
We have evidence of the development of a complex system of metrology in Sumer from about 3000 BCE, and multiplication and reciprocal (division) tables, tables of squares, square roots and cube roots, geometrical exercises and division problems from around 2600 BCE onwards. Later Babylonian tablets dating from about 1800 to 1600 BCE cover topics as varied as fractions, algebra, methods for solving linear, quadratic and even some cubic equations, and the calculation of regular reciprocal pairs (pairs of number which multiply together to give 60). One Babylonian tablet gives an approximation to √2 accurate to an astonishing five decimal places. Others list the squares of numbers up to 59, the cubes of numbers up to 32 as well as tables of compound interest. Yet another gives an estimate for π of 3 1⁄8 (3.125, a reasonable approximation of the real value of 3.1416).
The Babylonians also developed another revolutionary mathematical concept, something else that the Egyptians, Greeks and Romans did not have, a circle character for zero, although its symbol was really still more of a placeholder than a number in its own right.
We have evidence of the development of a complex system of metrology in Sumer from about 3000 BCE, and multiplication and reciprocal (division) tables, tables of squares, square roots and cube roots, geometrical exercises and division problems from around 2600 BCE onwards. Later Babylonian tablets dating from about 1800 to 1600 BCE cover topics as varied as fractions, algebra, methods for solving linear, quadratic and even some cubic equations, and the calculation of regular reciprocal pairs (pairs of number which multiply together to give 60). One Babylonian tablet gives an approximation to √2 accurate to an astonishing five decimal places. Others list the squares of numbers up to 59, the cubes of numbers up to 32 as well as tables of compound interest. Yet another gives an estimate for π of 3 1⁄8 (3.125, a reasonable approximation of the real value of 3.1416).
|
The idea of square numbers and quadratic equations (where the unknown quantity is multiplied by itself, e.g. x2) naturally arose in the context of the meaurement of land, and Babylonian mathematical tablets give us the first ever evidence of the solution of quadratic equations. The Babylonian approach to solving them usually revolved around a kind of geometric game of slicing up and rearranging shapes, although the use of algebra and quadratic equations also appears. At least some of the examples we have appear to indicate problem-solving for its own sake rather than in order to resolve a concrete practical problem.
The Babylonians used geometric shapes in their buildings and design and in dice for the leisure games which were so popular in their society, such as the ancient game of backgammon. Their geometry extended to the calculation of the areas of rectangles, triangles and trapezoids, as well as the volumes of simple shapes such as bricks and cylinders (although not pyramids). |
The famous and controversial Plimpton 322 clay tablet, believed to date from around 1800 BCE, suggests that the Babylonians may well have known the secret of right-angled triangles (that the square of the hypotenuse equals the sum of the square of the other two sides) many centuries before the Greek Pythagoras. The tablet appears to list 15 perfect Pythagorean triangles with whole number sides, although some claim that they were merely academic exercises, and not deliberate manifestations of Pythagorean triples.
Egyptian Mathematics
The early Egyptians settled along the fertile Nile valley as early as about 6000 BCE, and they began to record the patterns of lunar phases and the seasons, both for agricultural and religious reasons. The Pharaoh’s surveyors used measurements based on body parts (a palm was the width of the hand, a cubit the measurement from elbow to fingertips) to measure land and buildings very early in Egyptian history, and a decimal numeric system was developed based on our ten fingers. The oldest mathematical text from ancient Egypt discovered so far, though, is the Moscow Papyrus, which dates from the Egyptian Middle Kingdom around 2000 - 1800 BCE.
It is thought that the Egyptians introduced the earliest fully-developed base 10 numeration system at least as early as 2700 BCE (and probably much early). Written numbers used a stroke for units, a heel-bone symbol for tens, a coil of rope for hundreds and a lotus plant for thousands, as well as other hieroglyphic symbols for higher powers of ten up to a million. However, there was no concept of place value, so larger numbers were rather unwieldy (although a million required just one character, a million minus one required fifty-four characters).
Egyptian Mathematics
The early Egyptians settled along the fertile Nile valley as early as about 6000 BCE, and they began to record the patterns of lunar phases and the seasons, both for agricultural and religious reasons. The Pharaoh’s surveyors used measurements based on body parts (a palm was the width of the hand, a cubit the measurement from elbow to fingertips) to measure land and buildings very early in Egyptian history, and a decimal numeric system was developed based on our ten fingers. The oldest mathematical text from ancient Egypt discovered so far, though, is the Moscow Papyrus, which dates from the Egyptian Middle Kingdom around 2000 - 1800 BCE.
It is thought that the Egyptians introduced the earliest fully-developed base 10 numeration system at least as early as 2700 BCE (and probably much early). Written numbers used a stroke for units, a heel-bone symbol for tens, a coil of rope for hundreds and a lotus plant for thousands, as well as other hieroglyphic symbols for higher powers of ten up to a million. However, there was no concept of place value, so larger numbers were rather unwieldy (although a million required just one character, a million minus one required fifty-four characters).
|
The Rhind Papyrus, dating from around 1650 BCE, is a kind of instruction manual in arithmetic and geometry, and it gives us explicit demonstrations of how multiplication and division was carried out at that time. It also contains evidence of other mathematical knowledge, including unit fractions, composite and prime numbers, arithmetic, geometric and harmonic means, and how to solve first order linear equations as well as arithmetic and geometric series. The Berlin Papyrus, which dates from around 1300 BCE, shows that ancient Egyptians could solve second-order algebraic (quadratic) equations.
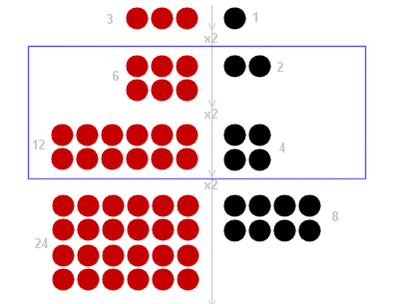
Multiplication, for example, was achieved by a process of repeated doubling of the number to be multiplied on one side and of one on the other, essentially a kind of multiplication of binary factors similar to that used by modern computers (see the example at right). These corresponding blocks of counters could then be used as a kind of multiplication reference table: first, the combination of powers of two which add up to the number to be multiplied by was isolated, and then the corresponding blocks of counters on the other side yielded the answer. This effectively made use of the concept of binary numbers, over 3,000 years before Leibniz introduced it into the west, and many more years before the development of the computer was to fully explore its potential. |
Practical problems of trade and the market led to the development of a notation for fractions. The papyri which have come down to us demonstrate the use of unit fractions based on the symbol of the Eye of Horus, where each part of the eye represented a different fraction, each half of the previous one (i.e. half, quarter, eighth, sixteenth, thirty-second, sixty-fourth), so that the total was one-sixty-fourth short of a whole, the first known example of a geometric series.
Unit fractions could also be used for simple division sums. For example, if they needed to divide 3 loaves among 5 people, they would first divide two of the loaves into thirds and the third loaf into fifths, then they would divide the left over third from the second loaf into five pieces. Thus, each person would receive one-third plus one-fifth plus one-fifteenth (which totals three-fifths, as we would expect).
The Egyptians approximated the area of a circle by using shapes whose area they did know. They observed that the area of a circle of diameter 9 units, for example, was very close to the area of a square with sides of 8 units, so that the area of circles of other diameters could be obtained by multiplying the diameter by 8⁄9 and then squaring it. This gives an effective approximation of π accurate to within less than one percent.
The pyramids themselves are another indication of the sophistication of Egyptian mathematics. Setting aside claims that the pyramids are first known structures to observe the golden ratio of 1 : 1.618 (which may have occurred for purely aesthetic, and not mathematical, reasons), there is certainly evidence that they knew the formula for the volume of a pyramid - 1⁄3 times the height times the length times the width - as well as of a truncated or clipped pyramid. They were also aware, long before Pythagoras, of the rule that a triangle with sides 3, 4 and 5 units yields a perfect right angle, and Egyptian builders used ropes knotted at intervals of 3, 4 and 5 units in order to ensure exact right angles for their stonework (in fact, the 3-4-5 right triangle is often called "Egyptian").
Speaking of Pythagoras, The Story of Maths will continue in Part II, as we move on to the Greeks!
Unit fractions could also be used for simple division sums. For example, if they needed to divide 3 loaves among 5 people, they would first divide two of the loaves into thirds and the third loaf into fifths, then they would divide the left over third from the second loaf into five pieces. Thus, each person would receive one-third plus one-fifth plus one-fifteenth (which totals three-fifths, as we would expect).
The Egyptians approximated the area of a circle by using shapes whose area they did know. They observed that the area of a circle of diameter 9 units, for example, was very close to the area of a square with sides of 8 units, so that the area of circles of other diameters could be obtained by multiplying the diameter by 8⁄9 and then squaring it. This gives an effective approximation of π accurate to within less than one percent.
The pyramids themselves are another indication of the sophistication of Egyptian mathematics. Setting aside claims that the pyramids are first known structures to observe the golden ratio of 1 : 1.618 (which may have occurred for purely aesthetic, and not mathematical, reasons), there is certainly evidence that they knew the formula for the volume of a pyramid - 1⁄3 times the height times the length times the width - as well as of a truncated or clipped pyramid. They were also aware, long before Pythagoras, of the rule that a triangle with sides 3, 4 and 5 units yields a perfect right angle, and Egyptian builders used ropes knotted at intervals of 3, 4 and 5 units in order to ensure exact right angles for their stonework (in fact, the 3-4-5 right triangle is often called "Egyptian").
Speaking of Pythagoras, The Story of Maths will continue in Part II, as we move on to the Greeks!
Ponder this
How did the notches used in prehistory evolved into symbols that represents amounts? How did we go from ///// to 5 to represent the idea of "five"?
Early mathematicians struggle with the idea of "zero", how would they represent "nothing" in practical, numerical terms?
Discuss
The development and advancement of early mathematics stems from practical needs (e.g. the need to tally livestock). Discuss how this need evolves from prehistory into the early Egyptian period. What drove them to create new mathematical knowledge, and how their use change within those individual periods. Did maths ever become an academic pursuit in those time? If not, why haven't they?
Further readings
Mathematics in Pre-History, a little primer with a good list of references for further reading.
Babylonian mathematics, the origins of Base 12 and our time-measuring system.
Ancient Egyptian mathematics, where the basis of geometry and fractions were developed.