|
In Part I we tackled the origins of arithmetic, the most basic and fundamental form of mathematics. Now we look at the more abstract world of geometry brought by the Greeks. It's no coincidence that at the same time they formulate mathematical theorems, they also ponder on philosophical paradoxes.
As we shall see, the Greeks idea of mathematics has more to do with attaining perfection than practical solutions. |
"In the Greek world mathematics was more closely related to philosophy than to practical affairs, and this kinship has persisted to the present day."
Carl B. Boyer, A History of Mathematics (1968)
As the Greek empire began to spread its sphere of influence into Asia Minor, Mesopotamia and beyond, the Greeks were smart enough to adopt and adapt useful elements from the societies they conquered. This was as true of their mathematics as anything else, and they adopted elements of mathematics from both the Babylonians and the Egyptians. But they soon started to make important contributions in their own right and, for the first time, we can acknowledge contributions by individuals. By the Hellenistic period, the Greeks had presided over one of the most dramatic and important revolutions in mathematical thought of all time.
The ancient Greek numeral system, known as Attic or Herodianic numerals, was fully developed by about 450 BCE, and in regular use possibly as early as the 7th Century BCE. It was a base 10 system similar to the earlier Egyptian one (and even more similar to the later Roman system), with symbols for 1, 5, 10, 50, 100, 500 and 1,000 repeated as many times needed to represent the desired number. Addition was done by totaling separately the symbols (1s, 10s, 100s, etc) in the numbers to be added, and multiplication was a laborious process based on successive doublings (division was based on the inverse of this process).
The ancient Greek numeral system, known as Attic or Herodianic numerals, was fully developed by about 450 BCE, and in regular use possibly as early as the 7th Century BCE. It was a base 10 system similar to the earlier Egyptian one (and even more similar to the later Roman system), with symbols for 1, 5, 10, 50, 100, 500 and 1,000 repeated as many times needed to represent the desired number. Addition was done by totaling separately the symbols (1s, 10s, 100s, etc) in the numbers to be added, and multiplication was a laborious process based on successive doublings (division was based on the inverse of this process).
|
But most of Greek mathematics was based on geometry. Thales, one of the Seven Sages of Ancient Greece, who lived on the Ionian coast of Asian Minor in the first half of the 6th Century BCE, is usually considered to have been the first to lay down guidelines for the abstract development of geometry, although what we know of his work (such as on similar and right triangles) now seems quite elementary.
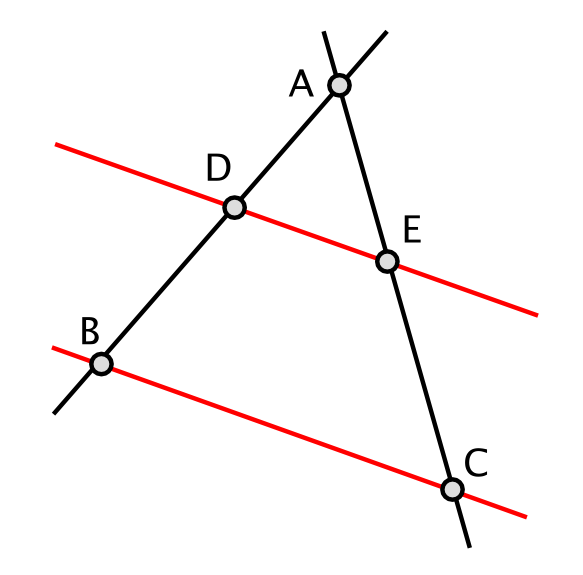
Thales established what has become known as Thales' Theorem, whereby if a triangle is drawn within a circle with the long side as a diameter of the circle, then the opposite angle will always be a right angle (as well as some other related properties derived from this). He is also credited with another theorem, also known as Thales' Theorem or the Intercept Theorem, about the ratios of the line segments that are created if two intersecting lines are intercepted by a pair of parallels (and, by extension, the ratios of the sides of similar triangles). |
To some extent, however, the legend of the 6th Century BCE mathematician Pythagoras of Samos has become synonymous with the birth of Greek mathematics. Indeed, he is believed to have coined both the words "philosophy" ("love of wisdom") and "mathematics" ("that which is learned"). Pythagoras was perhaps the first to realize that a complete system of mathematics could be constructed, where geometric elements corresponded with numbers. Pythagoras’ Theorem (or the Pythagorean Theorem) is one of the best known of all mathematical theorems. But he remains a controversial figure, as we will see, and Greek mathematics was by no means limited to one man.
Three geometrical problems in particular, often referred to as the Three Classical Problems, and all to be solved by purely geometric means using only a straight edge and a compass, date back to the early days of Greek geometry: “the squaring (or quadrature) of the circle”, “the doubling (or duplicating) of the cube” and “the trisection of an angle”. These intransigent problems were profoundly influential on future geometry and led to many fruitful discoveries, although their actual solutions (or, as it turned out, the proofs of their impossibility) had to wait until the 19th Century.
Hippocrates of Chios (not to be confused with the great Greek physician Hippocrates of Kos) was one such Greek mathematician who applied himself to these problems during the 5th Century BCE (his contribution to the “squaring the circle” problem is known as the Lune of Hippocrates). His influential book “The Elements”, dating to around 440 BCE, was the first compilation of the elements of geometry, and his work was an important source for Euclid's later work.
It was the Greeks who first grappled with the idea of infinity, such as described in the well-known paradoxes attributed to the philosopher Zeno of Elea in the 5th Century BCE. The most famous of his paradoxes is that of Achilles and the Tortoise, which describes a theoretical race between Achilles and a tortoise. Achilles gives the much slower tortoise a head start, but by the time Achilles reaches the tortoise's starting point, the tortoise has already moved ahead. By the time Achilles reaches that point, the tortoise has moved on again, etc, etc, so that in principle the swift Achilles can never catch up with the slow tortoise.
Three geometrical problems in particular, often referred to as the Three Classical Problems, and all to be solved by purely geometric means using only a straight edge and a compass, date back to the early days of Greek geometry: “the squaring (or quadrature) of the circle”, “the doubling (or duplicating) of the cube” and “the trisection of an angle”. These intransigent problems were profoundly influential on future geometry and led to many fruitful discoveries, although their actual solutions (or, as it turned out, the proofs of their impossibility) had to wait until the 19th Century.
Hippocrates of Chios (not to be confused with the great Greek physician Hippocrates of Kos) was one such Greek mathematician who applied himself to these problems during the 5th Century BCE (his contribution to the “squaring the circle” problem is known as the Lune of Hippocrates). His influential book “The Elements”, dating to around 440 BCE, was the first compilation of the elements of geometry, and his work was an important source for Euclid's later work.
It was the Greeks who first grappled with the idea of infinity, such as described in the well-known paradoxes attributed to the philosopher Zeno of Elea in the 5th Century BCE. The most famous of his paradoxes is that of Achilles and the Tortoise, which describes a theoretical race between Achilles and a tortoise. Achilles gives the much slower tortoise a head start, but by the time Achilles reaches the tortoise's starting point, the tortoise has already moved ahead. By the time Achilles reaches that point, the tortoise has moved on again, etc, etc, so that in principle the swift Achilles can never catch up with the slow tortoise.
Paradoxes such as this one and Zeno's so-called Dichotomy Paradox are based on the infinite divisibility of space and time, and rest on the idea that a half plus a quarter plus an eighth plus a sixteenth, etc, etc, to infinity will never quite equal a whole. The paradox stems, however, from the false assumption that it is impossible to complete an infinite number of discrete dashes in a finite time, although it is extremely difficult to definitively prove the fallacy. The ancient Greek Aristotle was the first of many to try to disprove the paradoxes, particularly as he was a firm believer that infinity could only ever be potential and not real.
Democritus, most famous for his prescient ideas about all matter being composed of tiny atoms, was also a pioneer of mathematics and geometry in the 5th - 4th Century BCE, and he produced works with titles like "On Numbers", "On Geometrics", "On Tangencies", "On Mapping" and "On Irrationals", although these works have not survived. We do know that he was among the first to observe that a cone (or pyramid) has one-third the volume of a cylinder (or prism) with the same base and height, and he is perhaps the first to have seriously considered the division of objects into an infinite number of cross-sections.
However, it is certainly true that Pythagoras in particular greatly influenced those who came after him, including Plato, who established his famous Academy in Athens in 387 BCE, and his protégé Aristotle, whose work on logic was regarded as definitive for over two thousand years. Plato the mathematician is best known for his description of the five Platonic solids, but the value of his work as a teacher and popularizer of mathematics can not be overstated.
Plato’s student Eudoxus of Cnidus is usually credited with the first implementation of the “method of exhaustion” (later developed by Archimedes), an early method of integration by successive approximations which he used for the calculation of the volume of the pyramid and cone. He also developed a general theory of proportion, which was applicable to incommensurable (irrational) magnitudes that cannot be expressed as a ratio of two whole numbers, as well as to commensurable (rational) magnitudes, thus extending Pythagoras’ incomplete ideas.
Perhaps the most important single contribution of the Greeks, though - and Pythagoras, Plato and Aristotle were all influential in this respect - was the idea of proof, and the deductive method of using logical steps to prove or disprove theorems from initial assumed axioms. Older cultures, like the Egyptians and the Babylonians, had relied on inductive reasoning, that is using repeated observations to establish rules of thumb. It is this concept of proof that give mathematics its power and ensures that proven theories are as true today as they were two thousand years ago, and which laid the foundations for the systematic approach to mathematics of Euclid and those who came after him.
Beyond Greece
By the 3rd Century BCE, in the wake of the conquests of Alexander the Great, mathematical breakthroughs were also beginning to be made on the edges of the Greek Hellenistic empire.
Democritus, most famous for his prescient ideas about all matter being composed of tiny atoms, was also a pioneer of mathematics and geometry in the 5th - 4th Century BCE, and he produced works with titles like "On Numbers", "On Geometrics", "On Tangencies", "On Mapping" and "On Irrationals", although these works have not survived. We do know that he was among the first to observe that a cone (or pyramid) has one-third the volume of a cylinder (or prism) with the same base and height, and he is perhaps the first to have seriously considered the division of objects into an infinite number of cross-sections.
However, it is certainly true that Pythagoras in particular greatly influenced those who came after him, including Plato, who established his famous Academy in Athens in 387 BCE, and his protégé Aristotle, whose work on logic was regarded as definitive for over two thousand years. Plato the mathematician is best known for his description of the five Platonic solids, but the value of his work as a teacher and popularizer of mathematics can not be overstated.
Plato’s student Eudoxus of Cnidus is usually credited with the first implementation of the “method of exhaustion” (later developed by Archimedes), an early method of integration by successive approximations which he used for the calculation of the volume of the pyramid and cone. He also developed a general theory of proportion, which was applicable to incommensurable (irrational) magnitudes that cannot be expressed as a ratio of two whole numbers, as well as to commensurable (rational) magnitudes, thus extending Pythagoras’ incomplete ideas.
Perhaps the most important single contribution of the Greeks, though - and Pythagoras, Plato and Aristotle were all influential in this respect - was the idea of proof, and the deductive method of using logical steps to prove or disprove theorems from initial assumed axioms. Older cultures, like the Egyptians and the Babylonians, had relied on inductive reasoning, that is using repeated observations to establish rules of thumb. It is this concept of proof that give mathematics its power and ensures that proven theories are as true today as they were two thousand years ago, and which laid the foundations for the systematic approach to mathematics of Euclid and those who came after him.
Beyond Greece
By the 3rd Century BCE, in the wake of the conquests of Alexander the Great, mathematical breakthroughs were also beginning to be made on the edges of the Greek Hellenistic empire.
|
In particular, Alexandria in Egypt became a great centre of learning under the beneficent rule of the Ptolemies, and its famous Library soon gained a reputation to rival that of the Athenian Academy. The patrons of the Library were arguably the first professional scientists, paid for their devotion to research. Among the best known and most influential mathematicians who studied and taught at Alexandria were Euclid, Archimedes, Eratosthenes, Heron, Menelaus and Diophantus.
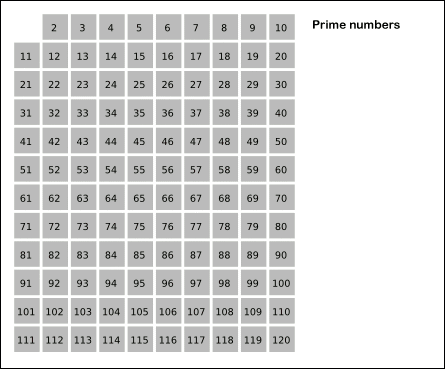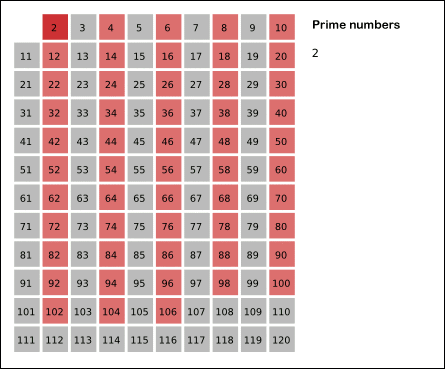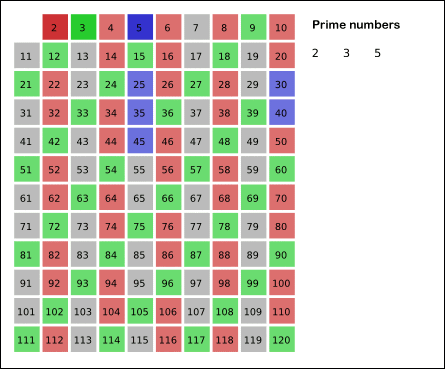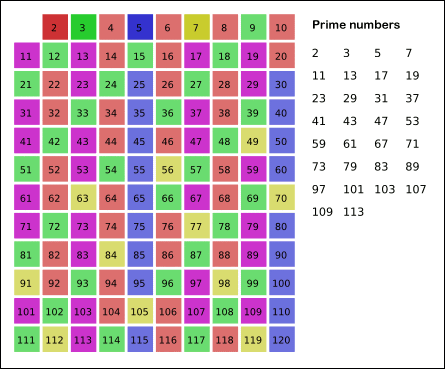
During the late 4th and early 3rd Century BCE, Euclid was the great chronicler of the mathematics of the time, and one of the most influential teachers in history. He virtually invented classical (Euclidean) geometry as we know it. Archimedes spent most of his life in Syracuse, Sicily, but also studied for a while in Alexandria. He is perhaps best known as an engineer and inventor but, in the light of recent discoveries, he is now considered of one of the greatest pure mathematicians of all time. Eratosthenes of Alexandria was a near contemporary of Archimedes in the 3rd Century BCE. A mathematician, astronomer and geographer, he devised the first system of latitude and longitude, and calculated the circumference of the earth to a remarkable degree of accuracy. As a mathematician, his greatest legacy is the “Sieve of Eratosthenes” algorithm for identifying prime numbers. |
It is not known exactly when the great Library of Alexandria burned down, but Alexandria remained an important intellectual centre for some centuries. In the 1st century BCE, Heron (or Hero) was another great Alexandrian inventor, best known in mathematical circles for Heronian triangles (triangles with integer sides and integer area), Heron’s Formula for finding the area of a triangle from its side lengths, and Heron’s Method for iteratively computing a square root. He was also the first mathematician to confront at least the idea of √-1 (although he had no idea how to treat it, something which had to wait for Tartaglia and Cardano in the 16th Century).
|
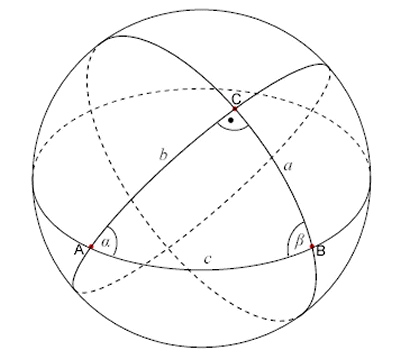
Menelaus of Alexandria, who lived in the 1st - 2nd Century CE, was the first to recognize geodesics on a curved surface as the natural analogues of straight lines on a flat plane. His book “Sphaerica” dealt with the geometry of the sphere and its application in astronomical measurements and calculations, and introduced the concept of spherical triangle (a figure formed of three great circle arcs, which he named "trilaterals").
In the 3rd Century CE, Diophantus of Alexandria was the first to recognize fractions as numbers, and is considered an early innovator in the field of what would later become known as algebra. He applied himself to some quite complex algebraic problems, including what is now known as Diophantine Analysis, which deals with finding integer solutions to kinds of problems that lead to equations in several unknowns (Diophantine equations). Diophantus’ “Arithmetica”, a collection of problems giving numerical solutions of both determinate and indeterminate equations, was the most prominent work on algebra in all Greek mathematics, and his problems exercised the minds of many of the world's best mathematicians for much of the next two millennia. |
But Alexandria was not the only centre of learning in the Hellenistic Greek empire. Mention should also be made of Apollonius of Perga (a city in modern-day southern Turkey) whose late 3rd Century BCE work on geometry (and, in particular, on conics and conic sections) was very influential on later European mathematicians. It was Apollonius who gave the ellipse, the parabola, and the hyperbola the names by which we know them, and showed how they could be derived from different sections through a cone.
Hipparchus, who was also from Hellenistic Anatolia and who live in the 2nd Century BCE, was perhaps the greatest of all ancient astronomers. He revived the use of arithmetic techniques first developed by the Chaldeans and Babylonians, and is usually credited with the beginnings of trigonometry. He calculated (with remarkable accuracy for the time) the distance of the moon from the earth by measuring the different parts of the moon visible at different locations and calculating the distance using the properties of triangles. He went on to create the first table of chords (side lengths corresponding to different angles of a triangle). By the time of the great Alexandrian astronomer Ptolemy in the 2nd Century CE, however, Greek mastery of numerical procedures had progressed to the point where Ptolemy was able to include in his “Almagest” a table of trigonometric chords in a circle for steps of ¼° which (although expressed sexagesimally in the Babylonian style) is accurate to about five decimal places.
By the middle of the 1st Century BCE and thereafter, however, the Romans had tightened their grip on the old Greek empire. The Romans had no use for pure mathematics, only for its practical applications, and the Christian regime that followed it even less so. The final blow to the Hellenistic mathematical heritage at Alexandria might be seen in the figure of Hypatia, the first recorded female mathematician, and a renowned teacher who had written some respected commentaries on Diophantus and Apollonius. She was dragged to her death by a Christian mob in 415 CE.
Hipparchus, who was also from Hellenistic Anatolia and who live in the 2nd Century BCE, was perhaps the greatest of all ancient astronomers. He revived the use of arithmetic techniques first developed by the Chaldeans and Babylonians, and is usually credited with the beginnings of trigonometry. He calculated (with remarkable accuracy for the time) the distance of the moon from the earth by measuring the different parts of the moon visible at different locations and calculating the distance using the properties of triangles. He went on to create the first table of chords (side lengths corresponding to different angles of a triangle). By the time of the great Alexandrian astronomer Ptolemy in the 2nd Century CE, however, Greek mastery of numerical procedures had progressed to the point where Ptolemy was able to include in his “Almagest” a table of trigonometric chords in a circle for steps of ¼° which (although expressed sexagesimally in the Babylonian style) is accurate to about five decimal places.
By the middle of the 1st Century BCE and thereafter, however, the Romans had tightened their grip on the old Greek empire. The Romans had no use for pure mathematics, only for its practical applications, and the Christian regime that followed it even less so. The final blow to the Hellenistic mathematical heritage at Alexandria might be seen in the figure of Hypatia, the first recorded female mathematician, and a renowned teacher who had written some respected commentaries on Diophantus and Apollonius. She was dragged to her death by a Christian mob in 415 CE.
Ponder this
Why did the Greeks use mathematics to solve philosophical questions?
What prerequisite development allowed for the emergence of mathematical thinking in Greece? Were there other examples of such in other parts of the world?
Discuss
Even though Greek mathematics originated from philosophical questions, were there any evidence that they had applied these principles to solve real world problems?
Further reading
Greek Mathematics, the the Ancient History Encyclopedia.
Aristotle and Mathematics, too see how the Greeks link mathematics to philosophy, from the Stanford Encyclopedia of Philosophy.
Philosophy of Mathematics, for a more general link between the two fields, from the Standford Encyclopedia of Philosophy.