"If I have seen further it is by standing on the shoulders of Giants." - Isaac Newton, letter to Robert Hooke (1676)
When we last left, our heroes Tycho Brahe and Johannes Kepler had deduced that some law governs the motion of celestial bodies. Brahe had taken painfullt detailed measurements and observations of the movements of planets, while Kepler used those measurements to predict the paths that they will take, turning prediction into a science for the first time in history.
Around the same time, a Florentine astronomer had entered into the services of the powerful Medici family of bankers, Galileo Galilei.
Around the same time, a Florentine astronomer had entered into the services of the powerful Medici family of bankers, Galileo Galilei.
Apart from what we are familiar with his story, Galileo’s contribution is not limited to the astronomical. In that sense he simply reaffirmed what Copernicus had discovered using the methods of Brahe and Kepler. What is more significant is that he was the first to put its application right here on Earth.
In a move that foreshadows later discoveries, Galileo applies mathematical proofs on observable, reproducible experiments. This is not coincidental as his job as the court astronomer of the Medici family, he is required to entertain his lord’s guests with clever and enlightening shows. An example of these include that of the isochronous periods of swinging pendulums (which was later adopted into clockmaking), timing of falling bodies of variable masses using inclined ramps of variable steepness, and of course the famous Tower of Pisa cannonball drop.
Each of these experiments are grounded on two very important principles in modern science: observability and reproducibility. And from these two principles comes a new approach in the scientific method empiricism.
Through his experiments Galileo proves, for the first time in measurable and observable ways, that time and gravity are natural laws that are inviolable. His pendulums had shown that periods of oscillation (later to be used to regulate clocks) are a factor of the effect of gravitational acceleration on mass, and therefore measurable and predictable. His investigations on falling bodies further supports this by the precise calculations of the rate of gravitational acceleration itself. Refer back to your physics textbook and compare the two equations which govern these experiments.
In a move that foreshadows later discoveries, Galileo applies mathematical proofs on observable, reproducible experiments. This is not coincidental as his job as the court astronomer of the Medici family, he is required to entertain his lord’s guests with clever and enlightening shows. An example of these include that of the isochronous periods of swinging pendulums (which was later adopted into clockmaking), timing of falling bodies of variable masses using inclined ramps of variable steepness, and of course the famous Tower of Pisa cannonball drop.
Each of these experiments are grounded on two very important principles in modern science: observability and reproducibility. And from these two principles comes a new approach in the scientific method empiricism.
Through his experiments Galileo proves, for the first time in measurable and observable ways, that time and gravity are natural laws that are inviolable. His pendulums had shown that periods of oscillation (later to be used to regulate clocks) are a factor of the effect of gravitational acceleration on mass, and therefore measurable and predictable. His investigations on falling bodies further supports this by the precise calculations of the rate of gravitational acceleration itself. Refer back to your physics textbook and compare the two equations which govern these experiments.
Galileo’s codified laws were unprecedented, and it did more than paving the way to empiricism, but also to unlock the language of the natural world: mathematics.
Fast forward to the mid-17th century, a time where the works and methods of Kepler and Galileo became a standard practice amongst natural philosophers (now known as ‘physicists’) along with those of the ancient Greeks. Two-thousand kilometers away from Florence, a 19 year old Englishman was admitted into the Trinity College of Cambridge University. The boy was a talented student and, like his heroes Galileo and Kepler, had an affinity towards astronomy – but unfortunately astrology and alchemy as well.
It was during his years at Cambridge that the young Isaac Newton had first pondered on the mechanics of the world. He kept a set of notes, now known as the quaestiones quaedam philosophicae (latin: “certain philosophical questions”), where he waxed pensive on gravity, physical motions, optics, colours and ‘corpuscles’ (i.e. atoms). These burning questions became the driving factor to his later discoveries in those very topics, however it is his studies in mathematics during this time that made it all possible as it was at this time that he began formulating what would later became calculus.
Calculus, in and of itself is rather impractical, it requires a level of conceptual thinking to make it applicable, say, in Kepler’s problem on the motion of celestial bodies. Kepler’s laws simply rationalizes Brahe’s observations, but this is just a descriptive application of mathematics in physics. What if we are to apply it in a prescriptive problem such as how fast a communication satellite must travel to maintain a stable orbit around the Earth? Where will it be a week from now if we we're to boost its speed by x m/s for y seconds?
Calculus does this by translating observations (or expected observations) into a mathematical function accounting for all variations, and allowing for calculations on that function to the most infinitesimal amounts. Such as in the case below, time, may it be in hours, minus, seconds or milliseconds.
Fast forward to the mid-17th century, a time where the works and methods of Kepler and Galileo became a standard practice amongst natural philosophers (now known as ‘physicists’) along with those of the ancient Greeks. Two-thousand kilometers away from Florence, a 19 year old Englishman was admitted into the Trinity College of Cambridge University. The boy was a talented student and, like his heroes Galileo and Kepler, had an affinity towards astronomy – but unfortunately astrology and alchemy as well.
It was during his years at Cambridge that the young Isaac Newton had first pondered on the mechanics of the world. He kept a set of notes, now known as the quaestiones quaedam philosophicae (latin: “certain philosophical questions”), where he waxed pensive on gravity, physical motions, optics, colours and ‘corpuscles’ (i.e. atoms). These burning questions became the driving factor to his later discoveries in those very topics, however it is his studies in mathematics during this time that made it all possible as it was at this time that he began formulating what would later became calculus.
Calculus, in and of itself is rather impractical, it requires a level of conceptual thinking to make it applicable, say, in Kepler’s problem on the motion of celestial bodies. Kepler’s laws simply rationalizes Brahe’s observations, but this is just a descriptive application of mathematics in physics. What if we are to apply it in a prescriptive problem such as how fast a communication satellite must travel to maintain a stable orbit around the Earth? Where will it be a week from now if we we're to boost its speed by x m/s for y seconds?
Calculus does this by translating observations (or expected observations) into a mathematical function accounting for all variations, and allowing for calculations on that function to the most infinitesimal amounts. Such as in the case below, time, may it be in hours, minus, seconds or milliseconds.
Calculus gave Newton the capability to not just describe planetary motions, but to allow us to imagine alternative solutions. In solving the problem, Newton uses Galileo’s gravitational constant and Kepler’s law of varying orbital speed to deduce that mass plays an important factor in the solution, of which calculus is used to apply varying speeds in the calculation of distances between the masses.
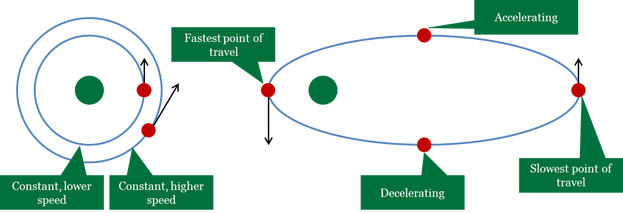
Let me explain: if distance = time x speed, and speed is constant, then the only factor that determines distance is time. Applying Galileo’s gravitational constant, this means that a satellite moving at constant speed will have a perfectly circular orbit. If speed varies, the orbit will skew the perfect circle into an elliptical path.
Let me explain: if distance = time x speed, and speed is constant, then the only factor that determines distance is time. Applying Galileo’s gravitational constant, this means that a satellite moving at constant speed will have a perfectly circular orbit. If speed varies, the orbit will skew the perfect circle into an elliptical path.
You can prove this with an experiment using a weight attached to a stretchable rubber cord. If you were to spin it around at constant speeds a circular ‘orbit’ will emerge, whether it’s fast or slow the shape of the orbit will maintain, only the distance between the weight and your hand will change. But if you change the speed as the weight spins the ‘orbit’ will be elliptical.
DISCLAIMER:
IFSA WILL NOT BE RESPONSIBLE FOR ANY INJURIES OR DAMAGE RESULTING FROM THIS EXPERIMENT.
PLEASE DON'T SUE US.
IFSA WILL NOT BE RESPONSIBLE FOR ANY INJURIES OR DAMAGE RESULTING FROM THIS EXPERIMENT.
PLEASE DON'T SUE US.
With this discovery through the application of calculus, Newton published his magnum opus, Philosophiæ Naturalis Principia Mathematica (latin: The Mathematical Principles of Natural Philosophy) and codified the Kepler’s laws and Galileo gravitational constant into his own laws of motion and universal gravitation using mathematical equations that are applicable to this day.
Some religious types were unhappy with this. They regard Newton’s discoveries as an affront to God, and taking away the mysteries and wonder of divine will. Though it’d be fitting if Newton were to tell them to “fly a kite”, he never did, cause haters gonna hate anyway.
We conclude Part 2 with the formalization of physics into mathematical principles. In Part 3, we will go beyond astronomy to something more relevant here on Earth.
Some religious types were unhappy with this. They regard Newton’s discoveries as an affront to God, and taking away the mysteries and wonder of divine will. Though it’d be fitting if Newton were to tell them to “fly a kite”, he never did, cause haters gonna hate anyway.
We conclude Part 2 with the formalization of physics into mathematical principles. In Part 3, we will go beyond astronomy to something more relevant here on Earth.
Ponder this
Although more known for his works in mathematics and physics Newton had delved into the occult, including but not limited to alchemy. How do you explain Newton's failure in applying his rigorous approach in physics to something as obscure as the alchemy?
Newton admitted to "standing on the shoulders of giants" such as Kepler and Galileo, and yet we know of only their work and nor how they derive it. One may argue for the benefit of efficiency and not having to reinvent the wheel; but are there any benefits to understanding the workings towards solved problems?
Discuss
Try having a read of the materials provided below, as well as those of Kepler's. Can you write a continuous development of a single idea from Kepler to Galileo to Newton? Maybe even show some mathematical proofs and improvements throughout their works?
Further readings
Dialogues Concerning Two New Sciences, Galileo’s work in the style of Plato’s Republic on the law of falling bodies, and gravitational acceleration.
Mathematical Principles of Natural Philosophy, 1846 English translation from the original Latin at Wikisource.
17th-century philosophy, article on the age that shaped the views of Galileo and Newton, at Wikipedia.